决策树

机器学习 算法
机器学习
发布日期:   2020-08-15
文章字数:   3.9k
阅读时长:   15 分

一、决策树模型与学习

  决策树是一种基本的分类与回归方法。决策树整体是一个树型结构，在分类的问题中，表示基于特征对实例进行分类的过程。可以认为是if-then的规则集合，也可以认为是定义在特征空间与类空间上的条件概率分布。
  优点是模型具有可读性，分类速度快。决策树学习通常分为三个步骤：特征选择、决策树生成和决策树的修剪。

  1. 学习时，可以利用训练数据，根据损失函数的最小化原则建立决策树模型。
  2. 预测时，对新的数据，利用决策树模型进行分类。

1.1 决策树模型

  定义1 （决策树）

  分类决策树模型是一种描述对实例点进行分类的树型结构。由结点(node)和有向边(directed edge)组成。结点有两种类型：内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性，叶节点表示一个类。
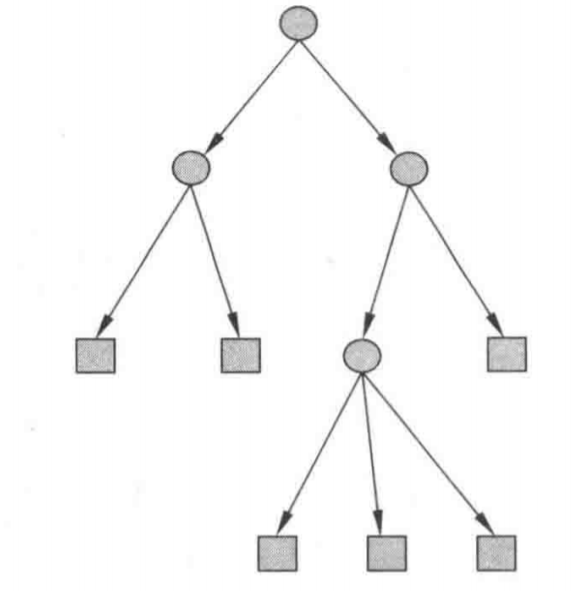
  利用决策树分类，从根节点开始，对某一特征进行测试，根据分类结果，将其分配到其子节点；如此递归进行测试并分配，直到叶节点，最后将实例分配到叶节点的类中。图1-1是一个决策树的示意图，圆表示内部节点，方框表示叶节点。

图1-1 决策树模型

1.2 决策树与if-then规则

  由决策树的根节点到叶节点的每一条路径构建一条规则；路径上的内部节点的特征对应着规则的条件，而叶节点的类对应着规则的结论。决策树的路径或其对应的if-then规则结合具有一个重要的性质：互斥且完备。即，每一个实例都被一条路径或规则覆盖，而且只被一条路径或规则覆盖。

1.3 决策树与条件概率分布

  决策树还表示为定义在给定的特征条件下的类的条件概率分布。这些条件概率分布定义在特征空间的一个划分上。决策树将特征空间划分为互不相交的单元(cell)，并在单元上定义了一个类的概率分布。决策树的一条路径对应了划分中的一个单元。
  假设 $X$ 为表示特征的随机变量，$Y$ 为表示类的随机变量，那么这个条件概率分布可以表示为 $P\left(Y|X\right)$。$X$ 的取值与给定的划分下单元的集合，$Y$ 取值于类的集合。各叶节点上的条件概率往往偏向某一个类的概率较大，决策树在分类时会将该实例分配到条件概率较大的那一类去。
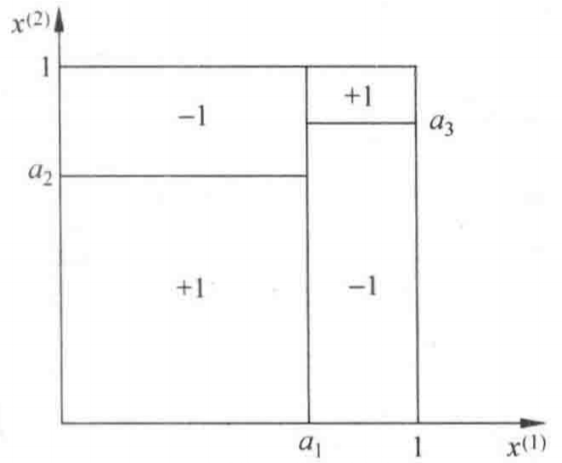
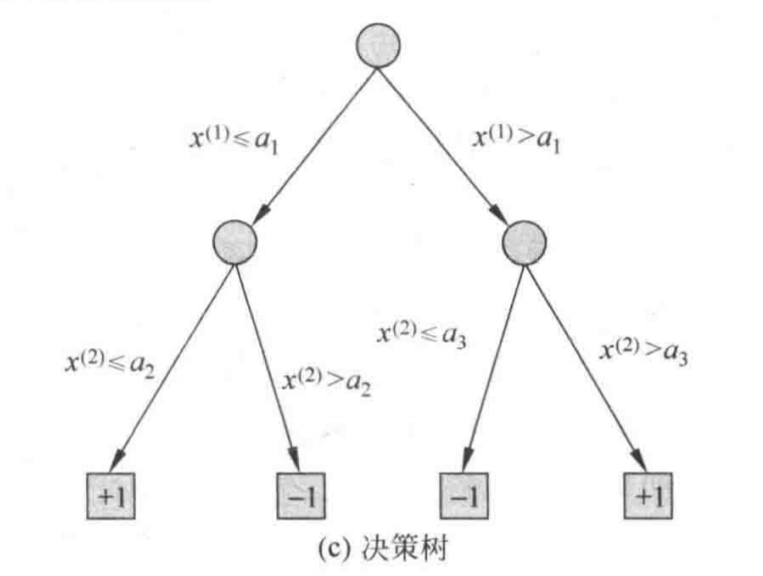
  图1-2表示了一种特征空间的划分与与之对应的决策树。

图1-2 决策树对应于条件概率分布

1.4 决策树学习

  假定给定训练数据集
$$
D=\left\{ \left( x_1,y_1 \right) ,\left( x_2,y_2 \right) ,\cdots ,\left( x_N,y_N \right) \right\}
$$
其中，$x_i=\left( x_{i}^{\left( 1 \right)},x_{i}^{\left( 2 \right)},\cdots ,x_{i}^{\left( n \right)} \right) ^{\text{T}}$ 为输入实例，$n$ 为特征个数，$y_i\in \left\{1,2,\cdots,K\right\}$ 为类标记，$i=1,2\cdots,N$，$N$ 为样本容量。决策树学习的目标是根据给定的训练数据集构建一个决策树模型，使其能够对新输入的实例进行正确分类。
  决策树的本质是从训练数据集中归纳出一组分类规则。与训练集相符的决策树可能有多个，也可能没有。目标是构建一个与训练数据集向矛盾较小的决策树，并且具有很好的泛化能力。
  决策树学习的损失函数通常是正则化的极大似然函数，学习策略的是以损失函数为目标函数的最小化。损失函数确定后，学习的目标变为在损失函数意义下的选择最优决策树的问题。因为从所有可能的决策树中选择合适的决策树属于 $NP$ 完全问题，因此实际中常常采用启发式方法，近似求解，这样得到的决策树为次最优的(sub-optimal)。
  决策树的学习算法通常是一个递归地选择最优特征，并根据该特征对训练数据进行分割，使得各个子数据集有一个最好的分类过程。这个过程也就是特征空间的划分，也是决策树的构建过程。然后递归分类，直到所有训练数据子集基本都被正确分类，这样就生成了一颗决策树。
  以上方法可能对训练数据集有一个很好的分类，但是对未知数据未必有很好的分类能力，很有可能发生过拟合的现象。因此我们需要对生成的树进行从叶到根进行剪枝，使树变得简单，由此拥有更好的泛化能力。具体做法是，去掉分类过于细致的叶节点，使其退回到父节点或更高的节点，然后将父节点或更高的节点变为叶节点。

二、特征选择

2.1 特征选择问题

  特征选择在于选择对数据集有分类能力的特征，以此提高决策树的效率。通常特征选择的标准是信息增益或信息增益比。

2.2 信息增益

  首先给出熵和条件熵的概念。

  熵(entopy)是表示随机变量不确定性的度量。设 $X$ 是表示随机变量不确定性的度量。设 $X$ 是一个取有限个值的离散随机变量，其概率分布为 $P\left(X=x_i\right)=p_i, i=1,2,\cdots,n$ 则随机变量 $X$ 的熵定义为
$$
H\left(X\right) = -\sum_{i=1}^n{p_i}\log p_i
$$
若 $p_i=0$，则定义 $0\log 0=0$。通常上式的对数以 $2$ 或 $e$ 为底，这是熵的单位分别称为比特(bit)或纳特(nat)。由定义知，熵只依赖于 $X$ 的分布，与 $X$ 的取值无关，所以也将 $X$ 的熵记作 $H\left(p\right)$，即
$$
H\left(p\right)=-\sum_{i=1}^np_i\log p_i
$$
  熵越大，随机变量的不确定性就越大。由定义可以验证
$$
0\le H\left(p\right)\le \log n
$$
  当随机变量只取两个值时，例如 $1,0$ 时，即 $X$ 的分布为
$$
P\left(X=1\right)=p,\; P\left(X=0\right)=1-p,\; 0\le p\le 1
$$
熵为
$$
H\left(p\right)=-\log_2p-\left(1-p\right)\log_2\left(1-p\right)
$$
这时，熵 $H\left(p\right)$随概率 $p$ 变化的曲线如图1-3所示（单位为比特）。

图1-3 伯努利分布熵与概率的关系

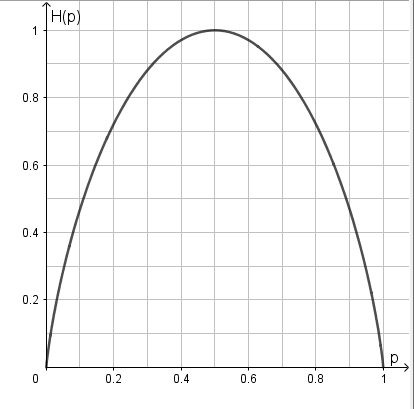
  当 $p=0$ 或 $p=1$ 时 $H\left(p\right)=0$，随机变量完全没有不确定性。当 $p=0.5$ 时，$H\left(p\right)=1$，熵取值最大，随机变量的不确定性最大。
  设有随机变量 $\left(X,Y\right)$，其联合概率分布为
$$
P\left(X=x_i,Y=y_i\right)=p_{ij},\; i=1,2,\cdots ,n; \; j=1,2,\cdots,m
$$
条件熵 $H\left(Y|X\right)$ 表示在已知随机变量 $X$ 的条件下随机变量 $Y$ 的不确定性。随机变量 $X$给定条件下随机变量 $Y$ 的条件熵 $H\left(Y|X\right)$，定义为 $X$ 给定条件下 $Y$ 的条件概率分布的熵对 $X$ 的数学期望
$$
H\left(Y|X\right)=\sum_{i=1}^n{p_iH\left(Y|X=x_i\right)}
$$
这里，$p_i=P\left(X=x_i\right)$，$i=1,2,\cdots,n$。
  当熵和条件熵中的概率由数据估计（一般是极大似然估计）得到时，所对应的熵和条件熵分别称为经验熵和经验条件熵。规定 $0\log 0=0$。
  信息增益表示得知特征 $X$ 的信息而使得类 $Y$ 的信息不确定性减小的程度。

  定义2 （信息增益）
  特征 $A$ 对训练数据集 $D$ 的信息增益 $g\left(D,A\right)$，定义为集合 $D$ 的经验熵 $H\left(D\right)$ 与特征 $A$ 给定条件下 $D$ 的经验条件熵 $H\left(D|A\right)$ 之差，即
$$
g\left(D,A\right)=H\left(D\right)-H\left(D|A\right)
$$
  决策树学习应用信息增益准则作为选择特征。对于给定的数据集 $D$ 和特征 $A$，经验熵 $H\left(D\right)$ 表示对数据集 $D$ 进行分类的不确定性。而经验条件熵 $H\left(D|A\right)$ 表示在特征 $A$ 给定条件下对数据集 $D$ 进行分类的不确定性。而二者的差，即信息增益，就是由于特征 $A$ 而使得对数据集 $D$ 的分类的不确定性的减少程度。显然，对于同一个数据集的不同特征，往往都有不同的信息增益，而信息增益大的特征具有更强的分类能力。

  算法 1（信息增益算法）

  输入：训练数据集 $D$ 和特征 $A$，$\left| D \right|$ 为样本容量，设有 $K$ 个类 $C_k$，$k=1,2,\cdots,K$，$\left| C_k \right|$ 为属于 $C_k$ 的样本个数，$\sum_{k=1}^K{\left|C_k\right|}=\left|D\right|$。设特征 $A$ 有 $n$ 个不同的取值 $\left\{a_1,a_2,\cdots,a_n\right\}$，根据特征 $A$ 的取值将 $D$ 划分为 $n$ 个子集 $D_1,D_2,\cdots,D_n$，$\left|D_i\right|$ 为 $D_i$ 的样本个数，$\sum_{i=1}^n{\left|D_i\right|}=\left|D\right|$;

  输出：特征 $A$ 对训练数据集 $D$ 的信息增益$g\left(D,A\right)$。

  1. 计算数据集 $D$ 的经验熵 $H\left(D\right)$;
    $$
    H\left( D \right) =-\sum_{k=1}^K{\frac{\left| C_k \right|}{\left| D \right|}\log _2}\frac{\left| C_k \right|}{\left| D \right|}
    $$

  2. 计算特征 $A$ 对数据集 $D$ 的经验条件熵 $H\left(D|A\right)$

$$
H\left( D |A\right) =\sum_{i=1}^n{\frac{\left| D_i \right|}{\left| D \right|}H\left( D_i \right)}=-\sum_{i=1}^n{\frac{\left| D_i \right|}{\left| D \right|}\sum_{k=1}^K{\frac{\left| D_{ik} \right|}{\left| D_i \right|}\log _2\frac{\left| D_{ik} \right|}{\left| D_i \right|}}}
$$

  1. 计算信息增益

$$
g\left(D,A\right)=H\left(D\right)-H\left(D|A\right)
$$

  Python代码如下

def calc_H_D(trainLabelArr):
    """
    计算数据集D的经验熵
    :param trainLabelArr:当前数据集的标签集
    :return: 经验熵
    """
    # 初始化为0
    H_D = 0
    # 将当前所有标签放入集合中，这样只要有的标签都会在集合中出现，且出现一次。
    # 遍历该集合就可以遍历所有出现过的标记并计算其Ck
    # 这么做有一个很重要的原因：首先假设一个背景，当前标签集中有一些标记已经没有了，比如说标签集中
    # 没有0（这是很正常的，说明当前分支不存在这个标签）。
    # 计算Cl和D并求和时，由于没有0，那么C0=0，此时C0/D0=0,log2(C0/D0) = log2(0)，事实上0并不在log的定义区间内，出现了问题
    # 所以使用集合的方式先知道当前标签中都出现了那些标签，随后对每个标签进行计算，如果没出现的标签那一项就
    # 不在经验熵中出现（未参与，对经验熵无影响），保证log的计算能一直有定义
    trainLabelSet = set([label for label in trainLabelArr])
    # 遍历每一个出现过的标签
    for i in trainLabelSet:
        # 计算|Ck|/|D|
        # trainLabelArr == i：当前标签集中为该标签的的位置
        # 例如a = [1, 0, 0, 1], c = (a == 1): c == [True, false, false, True]
        # trainLabelArr[trainLabelArr == i]：获得为指定标签的样本
        # trainLabelArr[trainLabelArr == i].size：获得为指定标签的样本的大小，即标签为i的样本
        # 数量，就是|Ck|
        # trainLabelArr.size：整个标签集的数量（也就是样本集的数量），即|D|
        p = trainLabelArr[trainLabelArr == i].size / trainLabelArr.size
        # 对经验熵的每一项累加求和
        H_D += -1 * p * np.log2(p)

    # 返回经验熵
    return H_D


def calcH_D_A(trainDataArr_DevFeature, trainLabelArr):
    """
    计算经验条件熵
    :param trainDataArr_DevFeature:切割后只有feature那列数据的数组
    :param trainLabelArr: 标签集数组
    :return: 经验条件熵
    """
    # 初始为0
    H_D_A = 0
    # 在featue那列放入集合中，是为了根据集合中的数目知道该feature目前可取值数目是多少
    trainDataSet = set([label for label in trainDataArr_DevFeature])

    # 对于每一个特征取值遍历计算条件经验熵的每一项
    for i in trainDataSet:
        # 计算H(D|A)
        # trainDataArr_DevFeature[trainDataArr_DevFeature == i].size / trainDataArr_DevFeature.size:|Di| / |D|
        # calc_H_D(trainLabelArr[trainDataArr_DevFeature == i]):H(Di)
        H_D_A += trainDataArr_DevFeature[trainDataArr_DevFeature == i].size / trainDataArr_DevFeature.size \
                 * calc_H_D(trainLabelArr[trainDataArr_DevFeature == i])
    # 返回得出的条件经验熵
    return H_D_A


def calcBestFeature(trainDataList, trainLabelList):
    """
    计算信息增益最大的特征
    :param trainDataList: 当前数据集
    :param trainLabelList: 当前标签集
    :return: 信息增益最大的特征及最大信息增益值
    """
    # 将数据集和标签集转换为数组形式
    trainDataArr = np.array(trainDataList)
    trainLabelArr = np.array(trainLabelList)

    # 获取当前特征数目，也就是数据集的横轴大小
    featureNum = trainDataArr.shape[1]

    # 初始化最大信息增益
    maxG_D_A = -1
    # 初始化最大信息增益的特征
    maxFeature = -1

    # 信息增益的算法：
    # 1.计算数据集D的经验熵H(D)
    H_D = calc_H_D(trainLabelArr)
    # 对每一个特征进行遍历计算
    for feature in range(featureNum):
        # 2.计算条件经验熵H(D|A)
        # 由于条件经验熵的计算过程中只涉及到标签以及当前特征，为了提高运算速度（全部样本
        # 做成的矩阵运算速度太慢，需要剔除不需要的部分），将数据集矩阵进行切割
        # 数据集在初始时刻是一个Arr = 60000*784的矩阵，针对当前要计算的feature，在训练集中切割下
        # Arr[:, feature]这么一条来，因为后续计算中数据集中只用到这个
        # trainDataArr[:, feature]:在数据集中切割下这么一条
        # trainDataArr[:, feature].flat：将这么一条转换成竖着的列表
        # np.array(trainDataArr[:, feature].flat)：再转换成一条竖着的矩阵，大小为60000*1（只是初始是
        # 这么大，运行过程中是依据当前数据集大小动态变的）
        trainDataArr_DevideByFeature = np.array(trainDataArr[:, feature].flat)
        # 3.计算信息增益G(D|A)    G(D|A) = H(D) - H(D | A)
        G_D_A = H_D - calcH_D_A(trainDataArr_DevideByFeature, trainLabelArr)
        # 不断更新最大的信息增益以及对应的feature
        if G_D_A > maxG_D_A:
            maxG_D_A = G_D_A
            maxFeature = feature
    return maxFeature, maxG_D_A

2.3 信息增益比

  以信息增益作为划分数据集的特征，存在偏向于选择取值较多的特征的问题。使用信息增益比(information gain ratio)可以对这个问题校正。也可以依据这个选择特征作为划分。
  定义3 （信息增益比）
  特征 $A$ 对训练数据集 $D$ 的信息增益比 $g_R\left(D,A\right)$，定义为其信息增益 $g\left(D,A\right)$ 与训练数据集 $D$ 关于特征 $A$ 的值的熵 $H_A\left(D\right)$ 之比，即
$$
g_R\left(D,A\right)=\cfrac{g\left(D,A\right)}{H_A\left(D\right)}
$$
其中，
$$
H_A\left( D \right) =-\sum_{i=1}^n{\frac{\left| D_i \right|}{\left| D \right|}\log _2}\frac{\left| D_i \right|}{\left| D \right|}
$$
$n$ 是特征 $A$ 取值的个数。

三、决策树的生成

3.1 ID3算法

  ID3算法的核心是在决策树各个节点上应用信息增益准则选择特征

文章作者: Demerzel
文章链接: https://demerzelsun12.github.io/2020/08/15/jue-ce-shu/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 Demerzel !
机器学习 算法
评论
  目录