2022-05-30

模式识别

第一章绪论

分类与聚类

有监督学习：分类

已知：训练样本，每个样本的所属类别。

目的：利用训练样本的学习分类器，对未知类别样本分类。 2. 无监督学习：聚类已知：训练样本未知：不知道样本的所属类别，甚至类别数量也未知。目的：利用无监督样本集，发现规律，对当前样本集合中样本进行分类。

只有一部分样本有标签：半监督学习，标签不可靠：弱监督学习

统计模式识别与结构模式识别

统计方法：将模型看做空间中的一个点，采用解析几何和概率论、数理统计的方法，判别输入模式的类别属性。

结构方法：将模式看做是由一些基本元素有组织的构成，利用形式语言和自动机理论对模式的结构进行分析和判别。

鉴别模型与产生式模型

鉴别模型：不同类别样本在特征空间中处于不同区域，学习 $g (x)$ ，对于不同区域输出不同值。

产生式模型：模式时随机分布在特征空间中的一个随机矢量，在不同位置出现的概率不同。根据模式在某点出现的概率来判断该点所属的类别。

第二章模式识别系统

模式识别系统构成：先“找到目标”，再“作出判别”。

综合滤波、投影、压缩等方法，获得相对通用、稳定有效的特征描述子。

HOG（特征描述子）+SVM行人检测

HOG：方向梯度直方图，利用图像边缘的方向密度分布描述图像特征

图片Gamma和颜色的归一化；
计算梯度；
构建直方图；
Block混叠空间块的归一化；
构建HOG特征描述子；
SVM训练；

SHIFT：尺度不变特征变换，改变旋转角度，图像亮度或拍摄视角，仍然能够得到好的检测效果

构建多尺度高斯差分DOG边缘图像序列
找到局部极值点，去除不对称、不清晰、不稳定的点作为特征点。
找到特征点主方向，梯度直方图描述

SIFT：尺度不变特征变换，改变旋转角度，图像亮度或拍摄视角，仍然能够得到好的检测效果

特征的比较与分类

将待识别样本x分类到与其最相似的类别中

输入：需要识别的样本x ；
计算x与所有类别的相似度 $s (x, ω_{i}) . i = 1, . . ., c$ ；
输出：相似度最大的类别 $ω_{j}$
$j = \arg max s (x, ω_{j})$
关键问题：如何度量样本x与类别 i 的相似程度？

模板匹配：

每个类别的“先验知识”就是一个样本（模板） $μ_{i}$

利用x与模板 $μ_{i}$ 的相似度，作为x与类别 $ω_{i}$ 的相似度

用距离度量样本之间相似度，一般用二范数：

s (x, μ) = - d (x, μ) = - ‖ x - μ ‖_{2}

最近邻分类器

每一个类别有多个训练样本 $D (x_{1}, . . ., x_{n_{i}})$ ，

输入：需要识别的样本x，训练样本集。

目标：寻找D中与x最近的样本y。

输出：y所属的类别。

缺点：计算量大，占用存储空间大，易受到样本噪声影响。

加速方法：

1.转为单模板加速，为每个类别的训练样本学习出一个模板 $μ$ ，思路，距离训练样本距离都比较近的点。

μ_{i} = \arg min \sum_{k = 1}^{n_{i}} d (x_{k}^{(i)}, μ), μ \in R^{d}

误差平方和准则函数：

J_{i} (μ) = \sum_{k = 1}^{n_{i}} ‖ x_{k}^{(i)} - μ ‖^{2}

极值点导数为0，

\nabla J_{i} (μ) = \sum_{k = 1}^{n_{i}} 2 (x_{k}^{(i) - μ} = 0

μ = \frac{1}{n} \sum_{k = 1}^{n_{i}} x_{k}^{(i)}

结论：计算每个类别训练样本的均值作为匹配模板。

2.多模板加速

使用多个模板，减少匹配次数

3.近邻剪辑

K近邻

选择距离最近的k个样本决定。

K的选择：过小，近似于最邻近分类。过大，引起分类误差。

常用距离函数：

街市距离
$d (x, y) = ‖ x - y ‖_{1} = \sum_{i = 1}^{n} | x_{i} - y_{i} |$
切比雪夫距离：
$d (x, y) = ‖ x - y ‖_{\infty} = max$

样本规格化

使样本每一个维特征均分布在相同的范围内。

均匀缩放，使得每个维度都缩放到 $[0, 1]$ 之间。
高斯缩放：假设每一维特征都符合高斯分布，平移、缩放为标准高斯分布。

加权距离

计算不同特征时，引入不同权重，克服量纲影响，体现不同特征重要性。

汉明距离：两个矢量对应位置元素不同的数量。

分类器性能评价

拒识率：只对有把握的样本判别类别，对没有把我的样本拒绝识别。设 M 个样本分类， $m_{r}$ 个被拒识， $m_{e}$ 个分类错误。

错误率： $P_{e} = \frac{m_{e}}{M - m_{r}}$ ，拒识率： $P_{r} = \frac{m_{r}}{m}$

召回率（查全率），相关信息中被检索出来的比例， $P_{s} = \frac{a}{a + b}$ ，准确率：检索到的信息，与主题相关的比例， $P = \frac{a}{a + c}$

评价方法：

两分法：随机将训练集划分为不相交两个子集。分别训练，测试，重复多次。
交叉验证：随机分成不相交的k个子集，使用k-1个训练，剩余用作测试。取平均
Bootstrap方法：样本集有放回的抽取n个样本，组成样本集A，B，集合A训练，B测试重复k次。

误差分析：

偏差：训练集的错误率。

方差：开发集错误与训练集错误的差值。

总误差，均方误差：偏差+方差

减小“可避免偏差”技术：

加大模型规模，是算法更好的拟合训练集
对训练集进行分析，根据结果修改输入特征：增加额外特征，消除特定类别的误差。引入正则化抵消方差。
减小或去除正则化。
修改模型

减小方差：

必须：
1. 增加更多训练数据。
2. 提前终止
常用的：
1. 计算成本不敏感是使用正则化
2. 样本少时进行特征选择
3. 降低计算成本时，减小模型规模

第三章特征选择与特征提取

降维

高维空间映射到地位空间
降低计算的复杂度
提高分类器性能

应用角度：

特征选择：从原始特征中直接挑选对分类最有价值的
特征提取将原始特征变换得到新的低维特征

特征分析数学基础：

分析样本集在特征空间中的分布情况：奇异值分解
内积矩阵：各样本之间的相似度（距离）
外积矩阵：各维特征的分布（协方差）

正态分布：

p (x) \sim N (μ, σ^{2}) p (x) = \frac{1}{\sqrt{2 π} σ} \exp [- \frac{1}{2} (\frac{x - μ}{σ})^{2}]

多元正态分布函数：

p (x) \sim N (μ, Σ) p (x) = \frac{1}{(2 π)^{d / 2} | Σ |^{1 / 2}} \exp [- \frac{1}{2} (x - μ)^{t} Σ^{- 1} (x - μ)]

均值： $μ = E (x) = \int x p (x) d x$

协方差矩阵：

Σ = E ((x - μ) (x - μ)^{t}) = \int (x - μ) (x - μ)^{t} p (x) d x σ_{i j} = E ((x_{i} - μ_{i}) (x_{j} - μ_{j}))

散布矩阵

样本x的散布矩阵：

S = \frac{1}{n} \sum_{s \in D} (x - m) (x - m)^{t} = \frac{1}{n} \sum_{s \in D} [(x_{i} - m_{i}) (x_{j} - m_{j})]_{d \times d}

类别可分判定依据

可分性依据：类内散布程度低，类间散布程度高。

类内距离准则：用每个样本与其所属类别中心之间距离平方和来度量。

类间距离准则：用每个类别的中心到样本整体中心之间的加权距离平方和度量。

证明散布准则。

特征选择：

从原始的特征集合 $X$ 中挑选出一组最有利于分类的特征 $X^{'}$

分支定界法：

判据单调性：对于两个特征子集 $X_{1}$ , $X_{2}$ ，

X_{1} \subset X_{2} \Rightarrow J (X_{1}) \subset J (X_{2})

当可分性判据满足单调性时，分支定界法才能够保证搜索到最优特征集合。

方法：

自顶向下构建搜索树，每条路径对应一种删除方式。

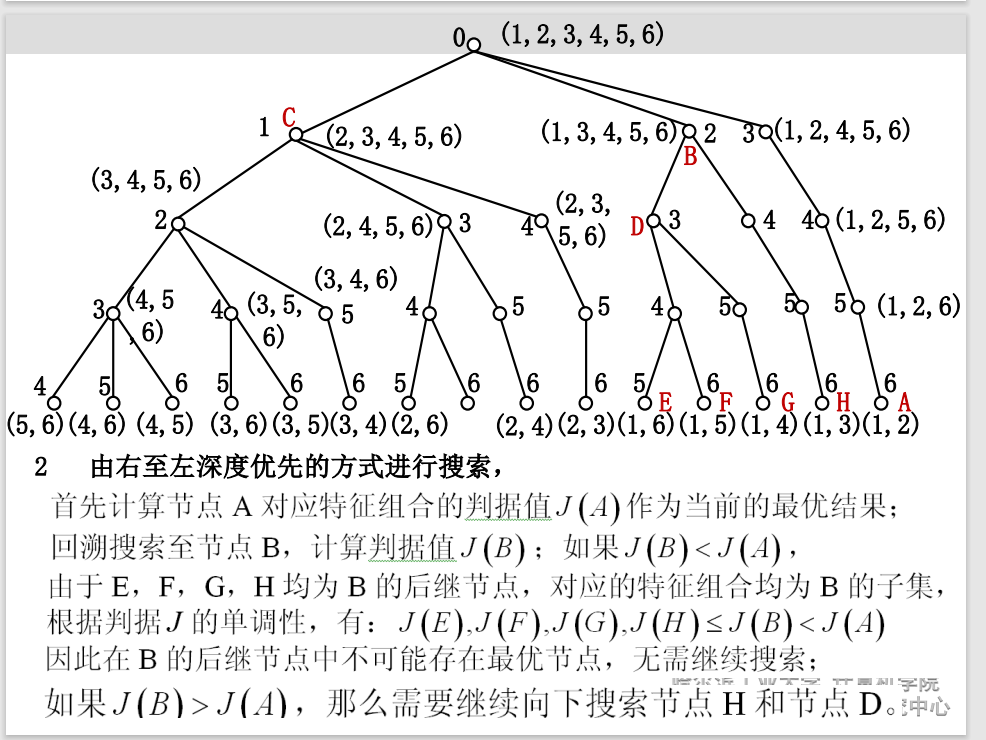
问题：

可分性判据必须具有单调性。不具有单调性则不能保证得到最优选择；
最优解分支位置决定计算复杂度。 ➢ 如果最优解分支在最右端并且根节点的子节点判据值均小于最优解，则搜索效率最高； ➢ 如果每个分支的可分性判据都大于其左端分支的可分性判据，实际的计算复杂度会超过穷举法。
计算量仍然可观。当原始的特征维数很大时，搜索到最优解需要的计算量仍然可观

次优搜索算法

顺序前进法（Sequential Forward Selection, SFS）

从一个空集开始每次向选择的特征集合中加入一个特征，直到特征集合中包含d’个特征为止，每次选择加入特征的原则：加入特征集后能够使得可分性判据最大。

每轮迭代只需要计算将每一个未被选择的特征加入 $X^{'}$ 之后的判据值，选择除d’个特征需要就散判据值的此时为：

\sum_{i = 0}^{d^{'} - 1} (d - i) = \frac{d^{'} (2 d - d^{'} + 1)}{2}

顺序后退法

每一轮从特征集中选择一个最差的特征删除，选择特征的原则是将其删除之后使得判据值下降最小。

\sum_{i = 0}^{d - d^{'} - 1} (d - i) = \frac{(d - d^{'}) (d + d^{'} + 1)}{2}

广义顺序前进（后退）法

每次增加或删除 r个特征

特征提取

特征选择：从原始x中选出若干维特征特征提取：对原始特征进行函数变换得到新特征

主成分分析PCA

PCA是一种最常用的线性成分分析方法；PCA的主要思想是寻找到数据的主轴方向，由主轴构成一个新的坐标系（维数可以比原维数低），然后数据由原坐标系向新的坐标系投影。

将数据集空间，压缩为一条过均值点的线。每个样本在直线上存在不同的投影，可以反映样本间的差异。

零维平方误差到一维平方误差：

J_{0} (m) = \sum_{k = 1}^{m} ‖ m - x_{k} ‖^{2} J_{1} (a_{1}, \dots, a_{n}, e) = \sum_{k = 1}^{n} ‖ (m + a_{k} e) - x_{k} ‖^{2}

\frac{\partial J_{1}}{\partial a_{k}} = \sum_{k = 1}^{n} a_{k}^{2} ‖ e ‖^{2} - 2 \sum_{k = 1}^{n} a_{k} e^{t} (x_{k} - m) + \sum_{k = 1}^{n} ‖ x_{k} - m ‖^{2} = 0 a_{k} = e^{t} (x_{k} - m)

只需把向量 $x_{k}$ 向过 m 的直线垂直投影就能得到最小方差

J_{1} (e) =